이상치 탐지 기법 중 하나, Extreme Studentized Deviation(ESD)
통계학을 공부하다 보면 이상치(Outlier)를 어떻게 정의하고 탐지할 수 있는지에 대한 여러 가지 방법을 접하게 됩니다. 그 중 하나로 만난 개념이 바로 Extreme Studentized Deviation (ESD) 입니다. 이 개념은 특히 정규분포를 가정한 데이터에서 이상치를 정량적으로 판단할 때 유용하게 쓰입니다.
ESD란 무엇인가요?
Extreme Studentized Deviation을 우리말로 풀이하자면, ‘극단적인 표준화 편차’ 정도로 이해할 수 있습니다. 여기서 핵심은 평균에서 얼마나 벗어나 있는지를 표준편차로 나눈 값(studentized deviation) 을 기준으로 하여, 그 중에서도 가장 극단적인 값(extreme) 을 찾아내는 것에 초점이 있습니다.
이 값을 계산해 보면 다음과 같은 형태가 됩니다.
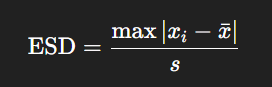
ESD = |x_i - x̄|의 최댓값 ÷ 표준편차 s
- x_i: 각 데이터 값
- x̄ : 평균
- s : 표준편차
즉, 평균에서 가장 많이 벗어난 데이터가 얼마나 극단적인지를 정량적으로 표현한 값이라고 볼 수 있습니다.
어디에 사용되나요?
ESD는 일반적으로 Generalized ESD Test라는 이상치 탐지 알고리즘에서 핵심 지표로 사용됩니다. 예를 들어, 최대 3개의 이상치가 존재할 수 있다고 가정한 후, 반복적으로 ESD 값을 계산하여 각 단계에서 가장 큰 ESD 값이 임계값(threshold)을 초과하는지를 확인하면서 이상치를 식별합니다.
이 알고리즘은 단순히 Z-score로 이상치를 판단하는 방법보다 더 견고하며, 여러 개의 이상치가 동시에 존재할 수 있는 데이터셋에서도 비교적 신뢰할 수 있는 결과를 제공합니다.
요약
Extreme Studentized Deviation은 Z-score와 유사하지만, 이상치 탐지 목적에 맞춰 가장 극단적인 값을 중심으로 계산하는 방법입니다. 평균에서 멀리 떨어진 정도를 표준편차 기준으로 정량화하고, 이를 통해 이상치 여부를 판단하는 데 유용합니다.
'자격증 (Certifications) > ADsP' 카테고리의 다른 글
| [ADsP] 결정계수(R²) (0) | 2025.05.18 |
|---|---|
| [ADsP] 반정형 데이터란? (0) | 2025.05.18 |
| [ADsP] 탐색적 데이터 분석(EDA) (0) | 2025.05.18 |
| [ADsP] 독립사건과 배반사건 (0) | 2025.05.18 |
| [ADsP] 유의수준과 유의확률 (0) | 2025.05.18 |